Voice Analysis: What Component Defines a Voice?
무엇이 음성을 정의하는가?
석사 연구 과정 동안 여러 기계에서 발생한 진동 신호를 분석해보았다. 이 포스트에는 진동 및 음성에 대하여 확인한 다양한 사항들을 업데이트할 예정이다.
소리의 3요소
주파수, 진폭, 파형. 이 세 가지가 소리의 특성을 정의한다는 사실은 오래전부터 알려져 있었다.
Harmonic과 파형
음성을 포함하여 다양한 진동 데이터를 주파수 영역에서 관찰할 때, 주요 진동수의 Harmonic을 관찰할 수 있다. Harmonic이란, 간단하게 말하면 배수 진동이라고 할 수 있다. 기계는 200Hz로 회전하고 있는데, 주파수 피크는 200Hz, 400Hz, 600Hz 등 200Hz의 정수배 주파수에서도 나타나며, 200Hz 에너지 수치가 Harmonic들에 비해 오히려 작을 수도 있다. 이 부분에 대해서 오랜 시간 의문을 가져왔지만 답을 얻지 못했었는데, 이번 Harmonic 현상을 관찰해보았다.
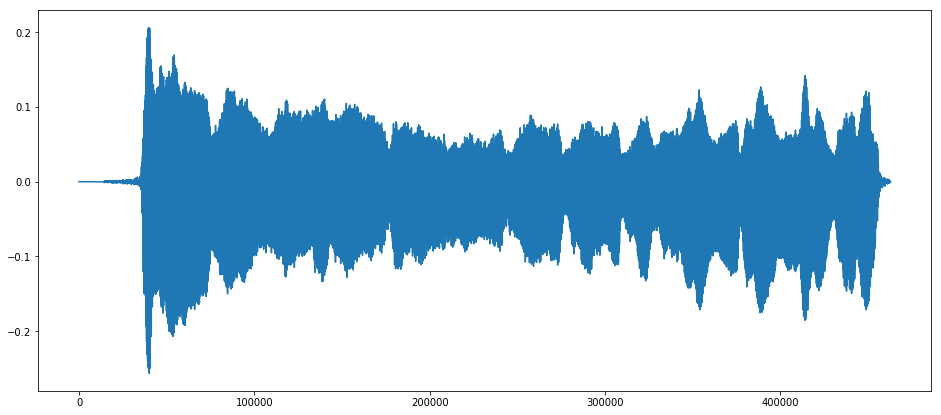
위 그래프는 연구자 본인의 “아” 발음을 녹음한 것이다.
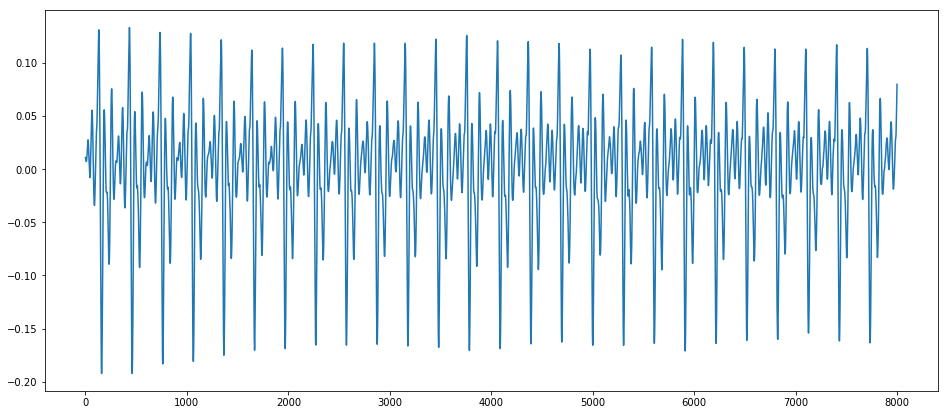
이 그래프는 위의 그래프를 조금 더 짧은 시간 구간으로 확대하여 나타낸 것이다. 확실치는 않지만 무엇인가가 반복되고 있다는 것은 확인할 수 있다.
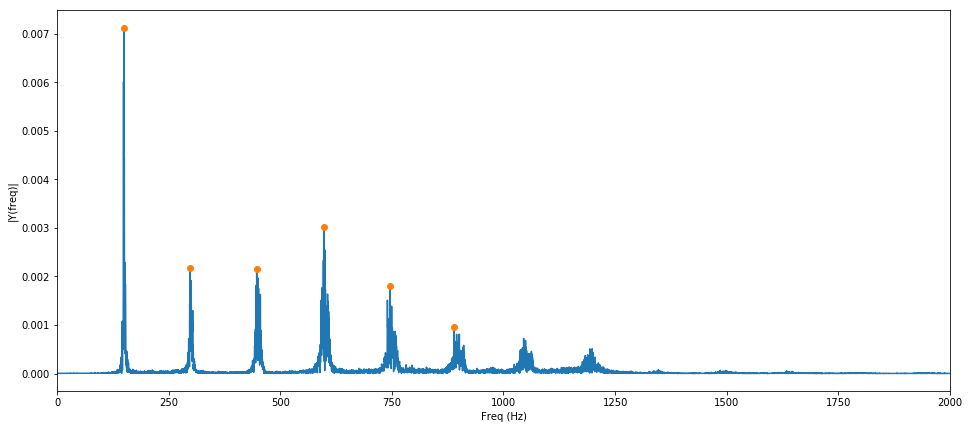
전체 구간에 대하여 FFT를 수행하여 그래프로 나타낸 결과가 위와 같다. 149Hz와 그 Harmonic이 존재하는 것을 확실하게 파악할 수 있다.
149Hz 단위로 음성을 쪼개서, 두 사이클마다 그래프로 나타낸 결과가 다음과 같다.
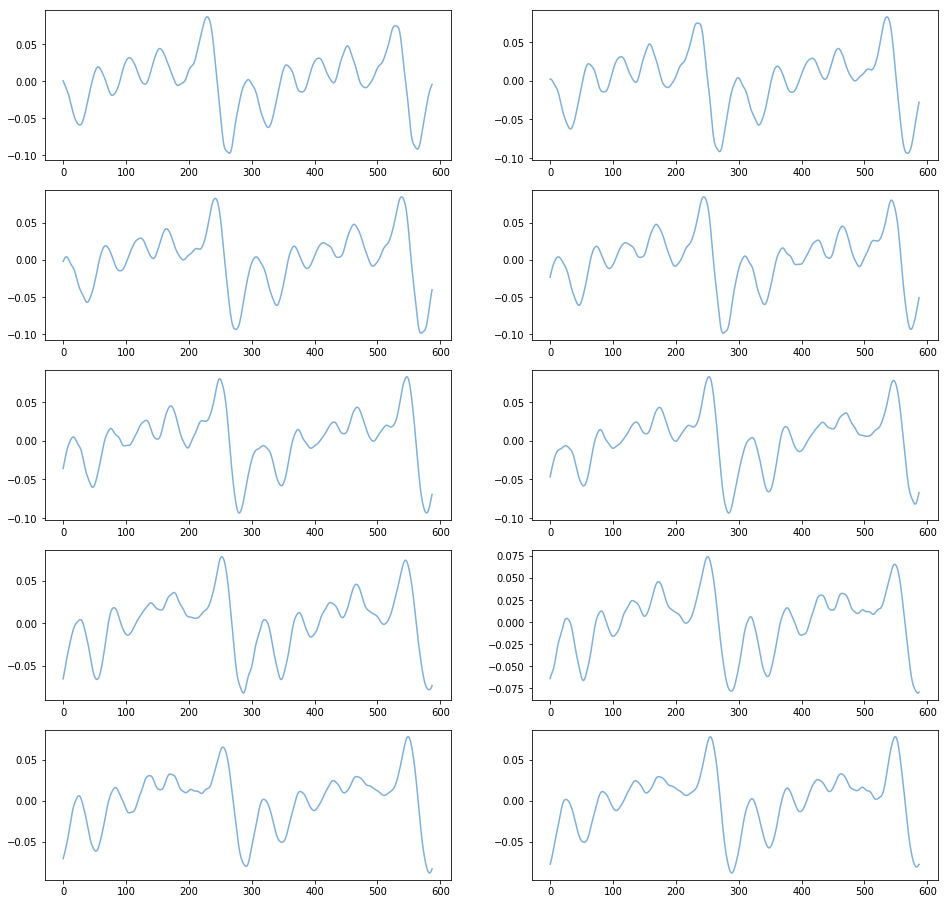
이제 149Hz에 해당하는 반복되는 패턴이 무엇인지 파악할 수 있다.
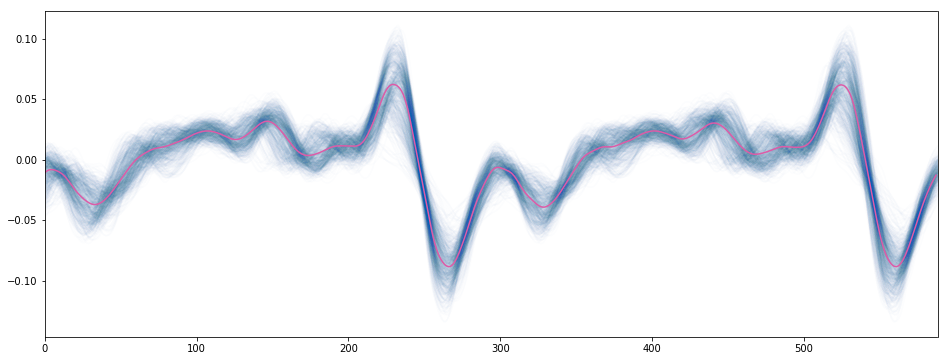
이 패턴을 겹쳐 그리면 다음과 같은 결과를 얻는다. 분홍색 선은 평균값을 나타낸다.
분홍색 신호만 반복되면 기계음에 더 가까운 소리가 난다.
가설: 음성은 확정적인 신호와 랜덤성이 가미되어 자연스러운 소리를 나타낸다.
Wavelet Transform을 이용한 분석
음성 데이터와 변위
음성 데이터와 일반적인 진동 데이터의 차이점 중의 하나는 물리적으로 계측하는 대상이 다르다는 점이다. 일반적인 진동 데이터는 가속도 센서를 이용하여 측정된다. 이는 산업용 진동 센서는 물론, 핸드폰에 내장되어 있는 가속도 센서에도 마찬가지다. 반면에 마이크나 스피커는 진동판의 변위를 계측하는 것으로 알고 있다.
음파가 공기 진동에 의해 변화하는 진동판의 변위를 그대로 재현하면 같은 소리를 낼 수 있다는 점은 당연하지만, 개인적으로는 신기하게 느껴지는 부분이다. 한편 가속도를 측정한 경우에도 측정된 가속도와 정확히 일치하는 가속도를 재현해낼 수 있다면, 동일한 진동을 구현할 수 있을 것이다. 가속도의 재현이라는 연구는 VR 시뮬레이션 분야에서 큰 의미를 가질 수 있을 듯 하나, 44.1kHz 단위로 진동을 재현하는 음성보다는 훨씬 낮은 주파수 단계에서의 재현이 주된 관심사일 것으로 추측된다. 아무튼 여기서 짚고 넘어가고자 하는 부분은 음성 데이터는 음파의 진폭을 계측한다는 점이다.
고등학교 교육 과정에서 진자의 변위, 속도, 가속도를 나타내는 그래프를 생각해보자. 변위, 속도, 가속도 세 가지가 모두 같은 주파수를 갖는 이유는 삼각함수가 적분에 의해 똑같은 주기성을 같는 cos <-> sin 변환을 나타내기 때문이다. 모든 신호는 삼각함수의 합으로 근사할 수 있고, 적분은 합에 대하여 독립적으로 적용되므로, 삼각함수의 합으로 표현된 가속도는 같은 주기성을 같는 속도와 가속도로 변환될 수 있다. 따라서 가속도를 계측하나, 속도를 계측하나, 변위를 계측하나 각 주파수의 에너지 비율은 동일할 것이다 (정말로 그럴까? 검증이 어렵지 않으므로 바로 확인해서 수정하도록 하자. ). -> 절대 아니다. 시간에 대해 미분한다고 했을 때, 주파수 term이 진폭에 곱해지므로 고주파일수록 미분시에 진폭이 더 커져야 한다.